第十三章：设计搜索自动完成系统 (Design A Search Autocomplete System)

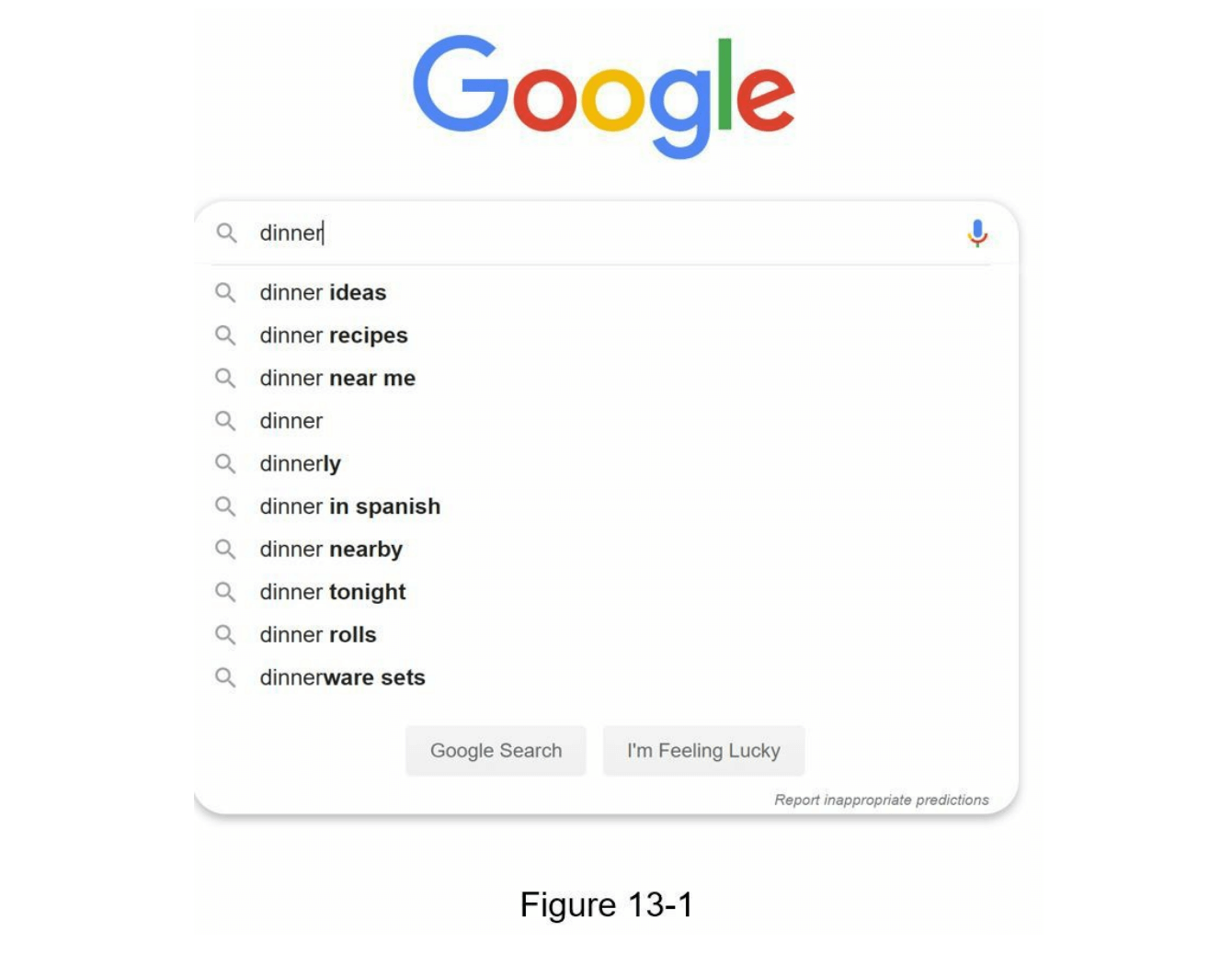
在使用Google搜索或在亚马逊购物时，当你在搜索框中输入内容时，会出现一个或多个与搜索词匹配的结果。这项功能被称为自动完成、输入建议、实时搜索或增量搜索。图13-1展示了Google搜索的一个例子，当输入“dinner”时，搜索框显示了一系列自动完成的结果。搜索自动完成是许多产品中的重要功能，这引出了一个面试问题：设计一个搜索自动完成系统，也称为“设计前k个结果”或“设计前k个最常搜索的查询”。

第 1 步 - 理解问题并确定设计范围

在应对系统设计面试问题时，第一步是通过提问来澄清需求。以下是一个候选人与面试官之间的对话示例：

候选人：匹配是否只支持在搜索查询的开头，还是也支持中间部分的匹配？
面试官：只支持在搜索查询的开头。

候选人：系统应返回多少个自动完成建议？
面试官：5个。

候选人：系统如何知道返回哪5个建议？
面试官：根据历史查询频率，按受欢迎程度决定。

候选人：系统是否支持拼写检查？
面试官：不支持拼写检查或自动纠正。

候选人：搜索查询是否是英语？
面试官：是的。如果时间允许，我们可以讨论多语言支持。

候选人：我们是否允许大写字母和特殊字符？
面试官：不允许，假设所有搜索查询都是小写的字母字符。

候选人：有多少用户使用该产品？
面试官：每日活跃用户数为1000万。

需求总结
以下是需求的总结：

• 快速响应时间：当用户输入搜索查询时，自动完成建议必须快速显示。根据Facebook自动完成系统的文章 [1]，系统需要在100毫秒内返回结果，否则会导致卡顿。
• 相关性：自动完成建议应与搜索词相关。
• 排序：系统返回的结果必须按受欢迎程度或其他排名模型排序。
• 可扩展性：系统能够处理高流量。
• 高可用性：当系统的某些部分离线、变慢或出现意外的网络错误时，系统应保持可用并可访问。

粗略估算

• 用户基数假设：

  • 假设每日活跃用户数（DAU）为1000万。
  • 平均每人每天进行10次搜索。

• 每条查询字符串的大小：

  • 假设使用ASCII字符编码，每个字符占1字节。
  • 假设每个查询包含4个单词，每个单词平均有5个字符。
  • 因此，每个查询约为4 x 5 = 20字节。

• 每个搜索的请求量：

  • 每个字符输入时，客户端都会向后端发送一次请求以获取自动完成建议。
  • 平均每个搜索会发送20次请求。例如，输入“dinner”时，用户发送了以下6次请求：
    • search?q=d
    • search?q=di
    • search?q=din
    • search?q=dinn
    • search?q=dinne
    • search?q=dinner

• 每秒查询请求数（QPS）：

  • 每秒查询请求数（QPS）估算：
    • 1000万用户 * 每天10次查询 * 每个查询20次请求 / 24小时 / 3600秒 ≈ 24,000 QPS。
  • 峰值QPS：由于搜索活动集中在特定时间段，假设峰值QPS是平均QPS的2倍，即 ≈ 48,000 QPS。

• 每日新增存储数据：

  • 假设20%的查询是新的：
    • 1000万用户 * 每天10次查询 * 每个查询20字节 * 20% ≈ 0.4 GB。
  • 这意味着每天有大约0.4GB的新数据需要添加到存储中。

第2步 - 提出高层设计并获得认可

在高层设计中，系统被分为两个主要组件：

1. 数据收集服务：该服务负责收集用户输入的查询，并实时聚合这些查询。尽管对于大规模数据集来说，实时处理并不现实，但这是一个很好的起点。在深入探讨中，我们将探索更具现实性的解决方案。
2. 查询服务：给定一个查询或前缀，返回最常被搜索的5个术语。

数据收集服务

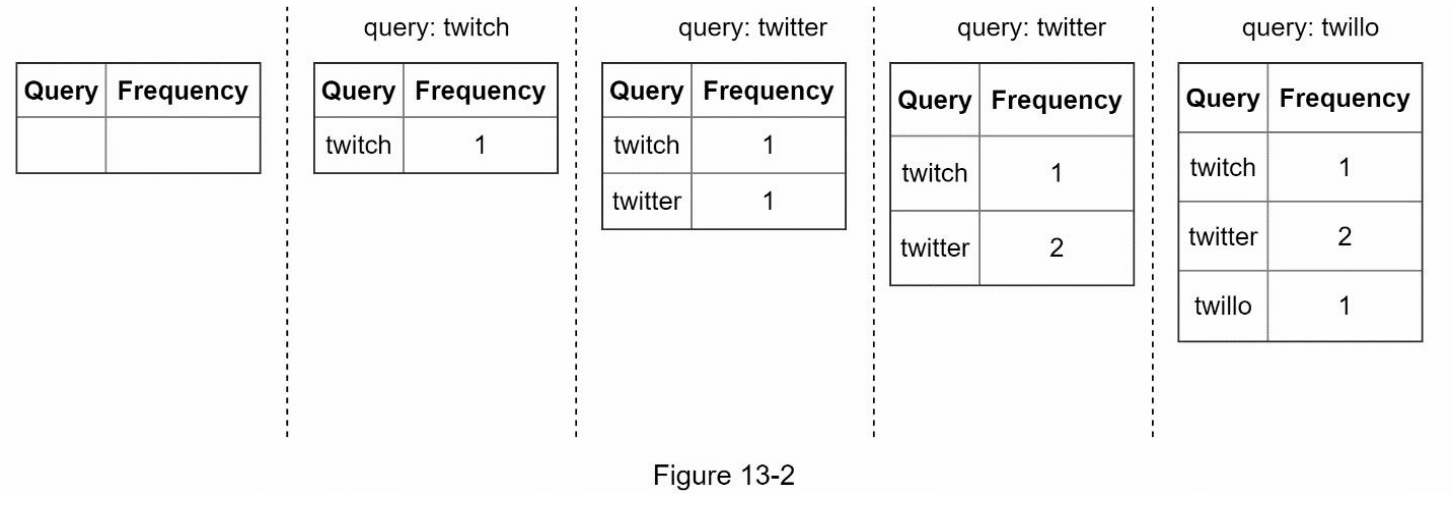
通过一个简化的例子来说明数据收集服务的工作原理。假设我们有一个频率表，用于存储查询字符串及其频率，如图13-2所示。一开始，频率表是空的。随后，用户依次输入查询“twitch”、“twitter”、“twitter”和“twillo”。图13-2显示了频率表如何更新。

查询服务

假设我们有一个频率表，如表13-1所示。它包含两个字段：

• Query（查询）：存储查询字符串。
• Frequency（频率）：表示查询被搜索的次数。

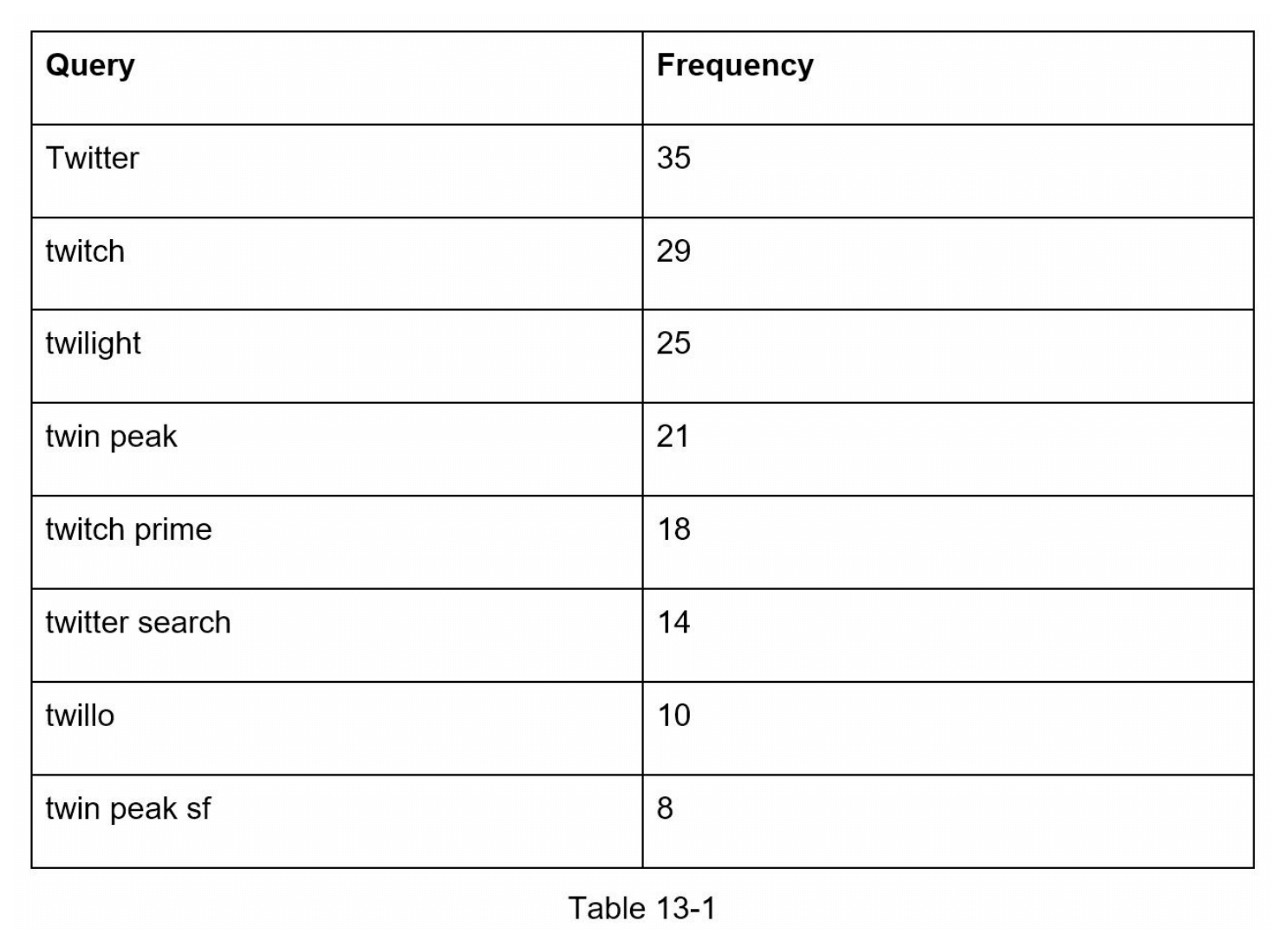
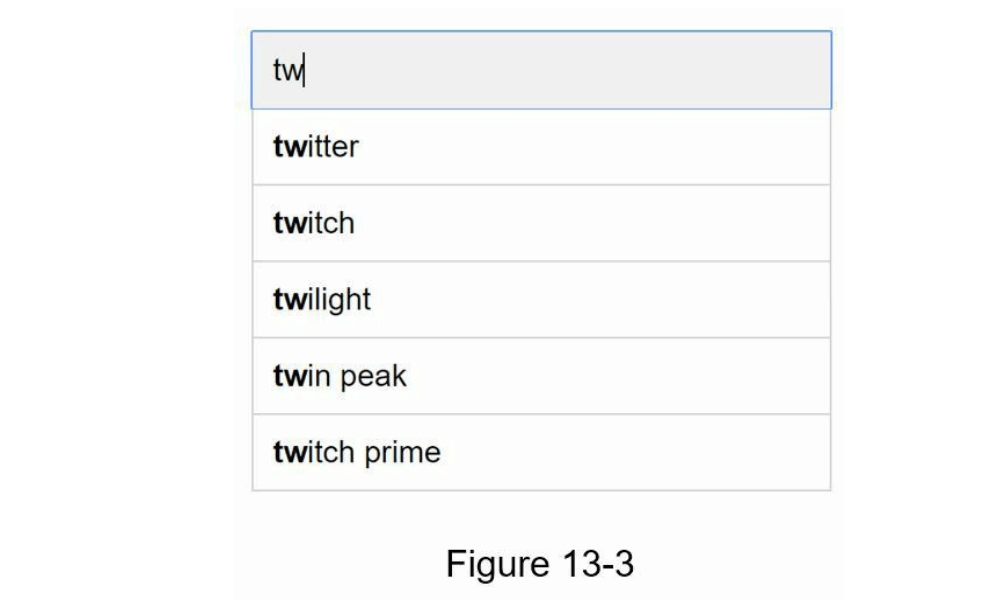
当用户在搜索框中输入“tw”时，假设频率表基于表13-1，系统会显示以下前5个搜索次数最多的查询（如图13-3所示）。

要获取最常搜索的前5个查询，可以执行以下SQL查询：

这种解决方案在数据集较小时是可以接受的，但当数据量较大时，频繁访问数据库会成为瓶颈。在深入探讨中，我们将研究如何进行优化，以提高系统的性能和扩展性。

第 3 步 - 深入设计

在高层设计中，我们讨论了数据收集服务和查询服务。虽然高层设计并不理想，但它作为一个良好的起点。在本节中，我们将深入探讨几个组件并探索优化方案，如下所示：

• 字典树数据结构
• 数据收集服务
• 查询服务
• 存储扩展
• 字典树操作

字典树数据结构 (Trie data structure)

在高层设计中，使用关系数据库进行存储。然而，从关系数据库中获取前 5 个搜索查询的效率较低。为了解决这个问题，使用了字典树（前缀树）数据结构。由于字典树数据结构对系统至关重要，我们将花费大量时间设计一个定制的字典树。请注意，其中的一些想法来自于文章 [2] 和 [3]。

理解基本的字典树数据结构对于这个面试问题是至关重要的。然而，这更像是一个数据结构问题，而不是系统设计问题。此外，许多在线资料解释了这一概念。在本章中，我们将仅讨论字典树数据结构的概述，并重点关注如何优化基本的字典树以提高响应时间。

字典树（发音为“try”）是一种树状数据结构，能够紧凑地存储字符串。其名称源自单词“检索”，表示它是为字符串检索操作设计的。字典树的主要思想包括以下几点：

• 字典树是一种树状数据结构。
• 根节点表示一个空字符串。
• 每个节点存储一个字符，并有 26 个子节点，分别对应每个可能的字符。为了节省空间，我们不绘制空链接。
• 每个树节点代表一个单词或前缀字符串。

图 13-5 显示了一个包含搜索查询“tree”、“try”、“true”、“toy”、“wish”、“win”的字典树。搜索查询以较粗的边框突出显示。

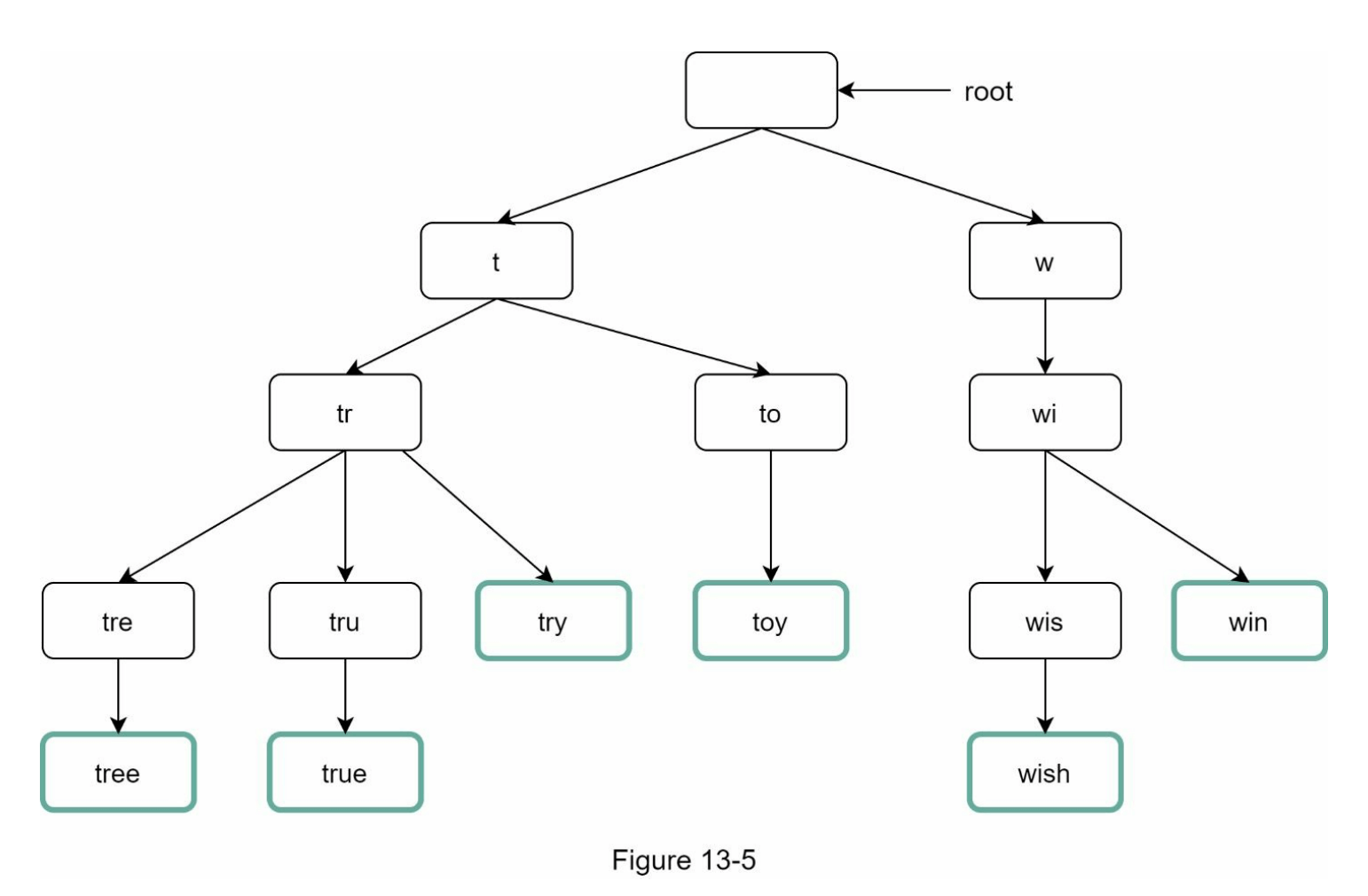
基本的字典树数据结构在节点中存储字符。为了支持按频率排序，频率信息需要包含在节点中。假设我们有以下频率表。

在节点中添加频率信息后，更新后的字典树数据结构如图 13-6 所示。

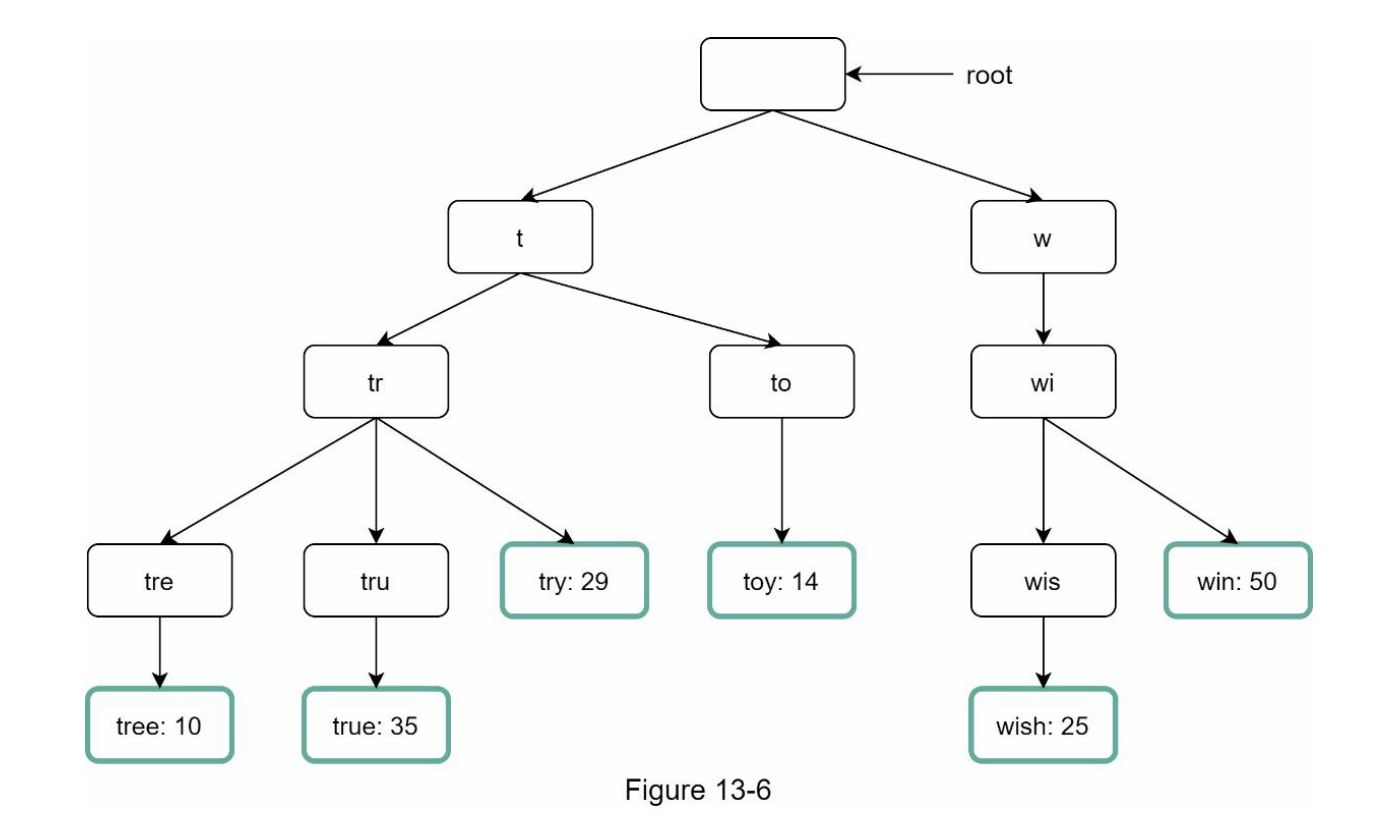
字典树是如何实现自动补全的？在深入算法之前，让我们定义一些术语。

• p：前缀的长度
• n：字典树中的节点总数
• c：给定节点的子节点数量

获取前 k 个最常搜索查询的步骤如下：

1. 查找前缀。时间复杂度：O(p)。
2. 从前缀节点遍历子树，以获取所有有效子节点。有效的子节点是能够形成有效查询字符串的节点。时间复杂度：O(c)。
3. 对子节点进行排序并获取前 k 个。时间复杂度：O(c log c)。

让我们用图 13-7 中的一个例子来解释这个算法。假设 k 等于 2，用户在搜索框中输入“tr”。算法的工作步骤如下：

• 步骤 1：查找前缀节点“tr”。
• 步骤 2：遍历子树以获取所有有效子节点。在这种情况下，节点 [tree: 10]、[true: 35] 和 [try: 29] 是有效的。
• 步骤 3：对子节点进行排序并获取前 2 个查询。前缀为“tr”的前 2 个查询是 [true: 35] 和 [try: 29]。

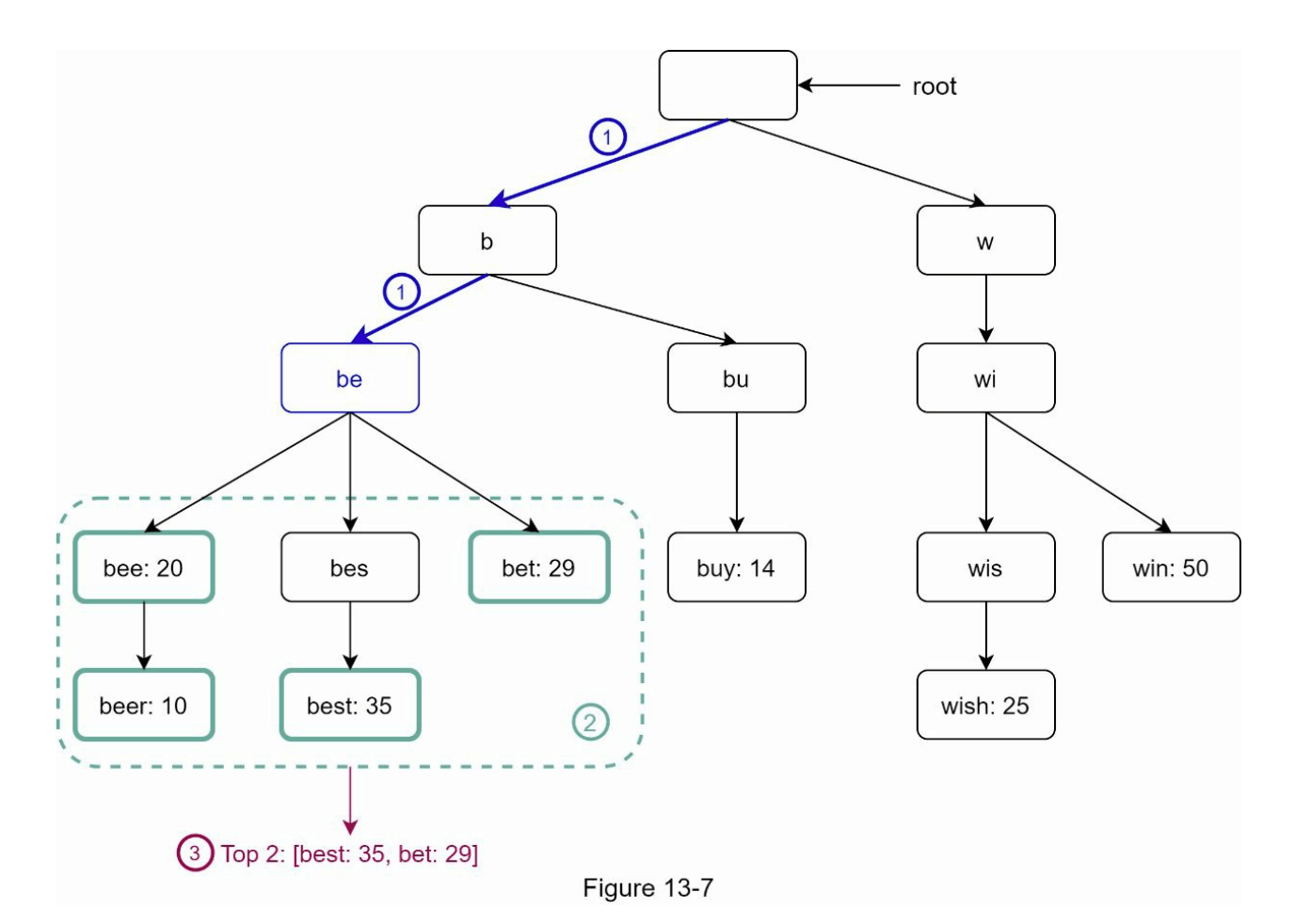
该算法的时间复杂度是上述每个步骤所花费时间的总和：O(p) + O(c) + O(c log c)

上述算法是直接的，但在最坏情况下需要遍历整个字典树以获取前 k 个结果，因此速度太慢。以下是两种优化方案：

1. 限制前缀的最大长度
2. 在每个节点缓存前搜索查询

让我们逐一看看这些优化。

限制前缀的最大长度

用户很少在搜索框中输入长搜索查询。因此，可以安全地说，p 是一个小整数，例如 50。如果我们限制前缀的长度，“查找前缀”的时间复杂度可以从 O(p) 降低到 O(小常数)，即 O(1)。

在每个节点缓存前搜索查询

为了避免遍历整个字典树，我们在每个节点上存储前 k 个最常用的查询。由于 5 到 10 个自动补全建议就足够满足用户需求，k 是一个相对较小的数字。在我们具体的情况下，仅缓存前 5 个搜索查询。

通过在每个节点缓存前搜索查询，我们显著减少了检索前 5 个查询的时间复杂度。然而，这种设计需要大量的空间来存储每个节点上的前查询。用空间换时间是非常值得的，因为快速响应时间非常重要。

图 13-8 显示了更新后的字典树数据结构。每个节点上存储前 5 个查询。例如，前缀为“be”的节点存储以下内容：[best: 35, bet: 29, bee: 20, be: 15, beer: 10]。

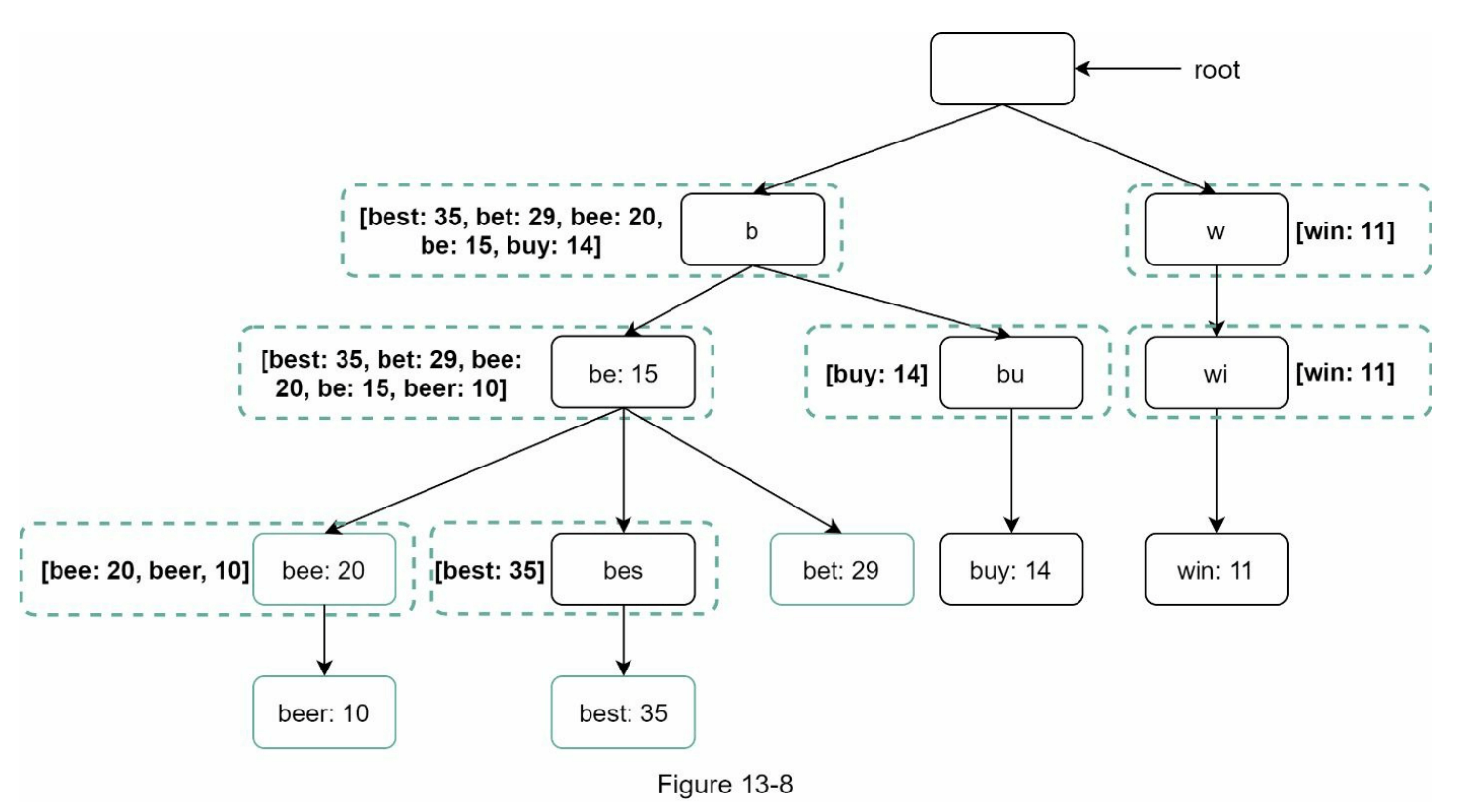
在应用这两种优化后，让我们重新审视算法的时间复杂度：

1. 查找前缀节点。时间复杂度：O(1)
2. 返回前 k 个查询。由于前 k 个查询已被缓存，这一步的时间复杂度为 O(1)。

由于每个步骤的时间复杂度均降低到 O(1)，我们的算法只需 O(1) 的时间即可获取前 k 个查询。

数据收集服务

在我们之前的设计中，每当用户输入搜索查询时，数据会实时更新。该方法并不实用，原因有两个：

• 用户每天可能会输入数十亿条查询。每个查询都更新字典树会显著降低查询服务的速度。
• 一旦字典树建立，前几个建议可能不会有太大变化。因此，频繁更新字典树是没有必要的。

为了设计一个可扩展的数据收集服务，我们需要检查数据的来源以及数据的使用方式。像 Twitter 这样的实时应用程序需要最新的自动补全建议。然而，许多 Google 关键字的自动补全建议可能在日常情况下变化不大。

尽管使用案例存在差异，但数据收集服务的基本基础保持不变，因为用于构建字典树的数据通常来自分析或日志服务。

图 13-9 显示了重新设计的数据收集服务。每个组件将逐一进行检查。

分析日志 (Analytics Logs)

分析日志存储有关搜索查询的原始数据。日志是仅附加的，不进行索引。表 13-3 显示了日志文件的示例。

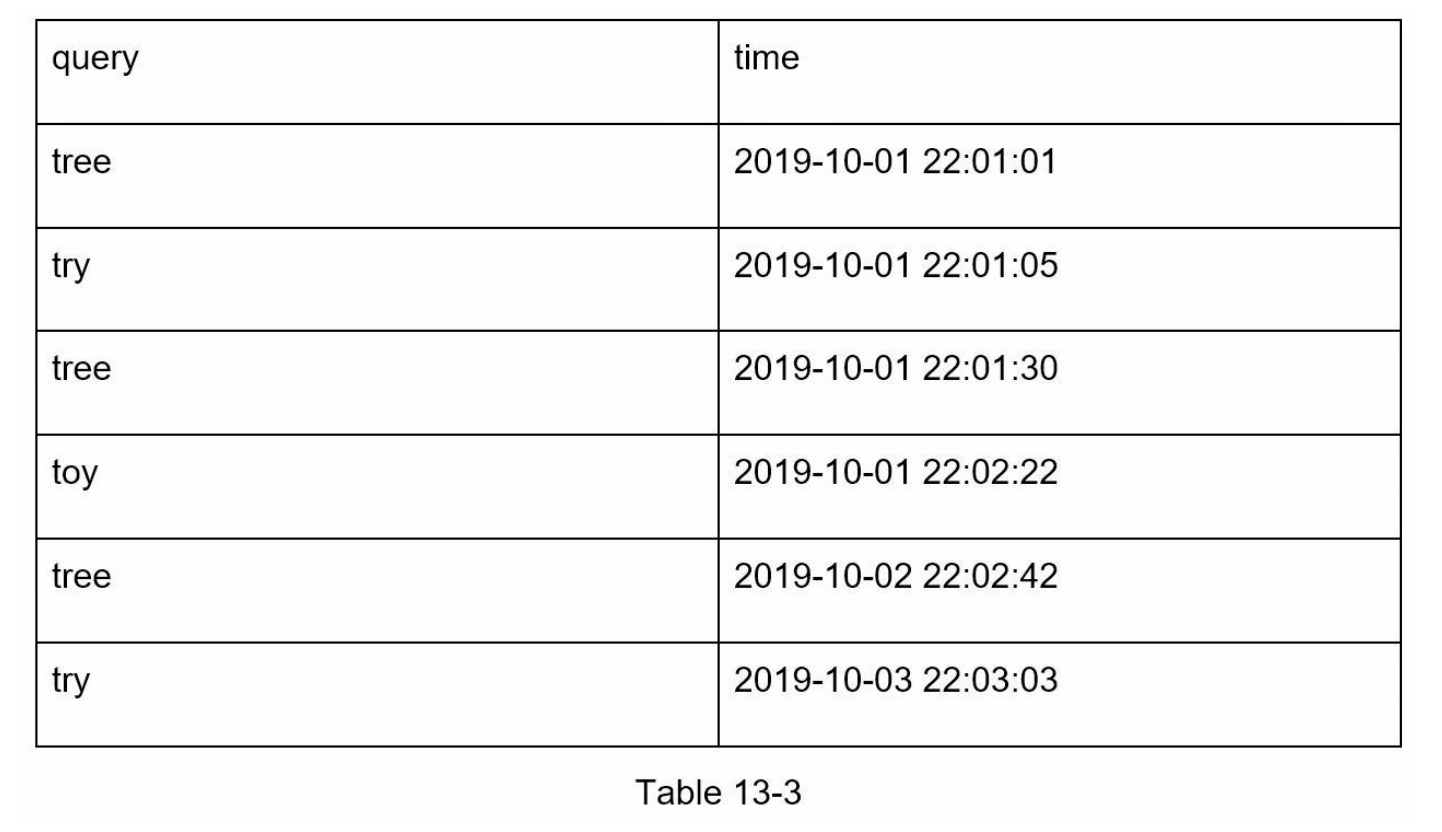
聚合器 (Aggregators)

分析日志的大小通常非常庞大，并且数据格式不正确。我们需要对数据进行聚合，以便系统能够轻松处理。根据使用案例的不同，我们可能会以不同的方式聚合数据。对于 Twitter 等实时应用程序，我们以较短的时间间隔聚合数据，因为实时结果非常重要。另一方面，对于许多使用案例，每周聚合一次数据可能就足够了。在面试过程中，验证实时结果是否重要。我们假设字典树每周重建一次。

聚合数据 (Aggregated Data)

表 13-4 显示了聚合的每周数据示例。“time”字段表示一周的开始时间。“frequency”字段是该周对应查询出现次数的总和。

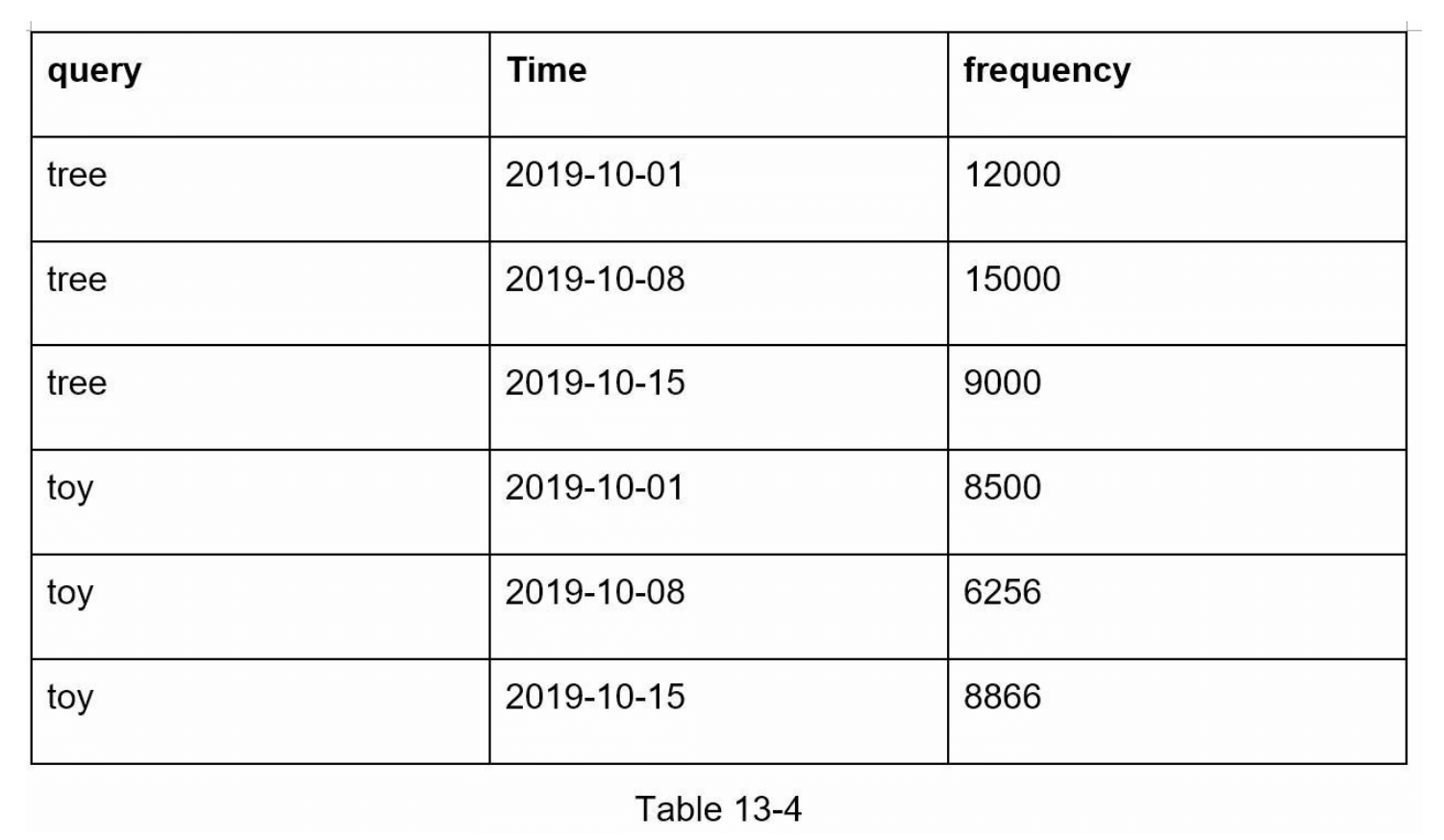
工作节点 (Workers)

工作节点是一组服务器，定期执行异步任务。它们构建字典树数据结构并将其存储在字典树数据库（Trie DB）中。

字典树缓存 (Trie Cache)

字典树缓存是一个分布式缓存系统，将字典树保存在内存中以实现快速读取。它每周对数据库进行快照。

字典树数据库（Trie DB）

字典树数据库是持久存储。有两种选项可用于存储数据：

1. 文档存储：由于每周构建新的字典树，我们可以定期对其进行快照、序列化并将序列化的数据存储在数据库中。像 MongoDB [4] 这样的文档存储非常适合序列化数据。

2. 键值存储：通过应用以下逻辑，字典树可以以哈希表形式表示 [4]：

   • 字典树中的每个前缀都映射到哈希表中的一个键。
   • 每个字典树节点上的数据映射到哈希表中的一个值。

图 13-10 显示了字典树与哈希表之间的映射关系。

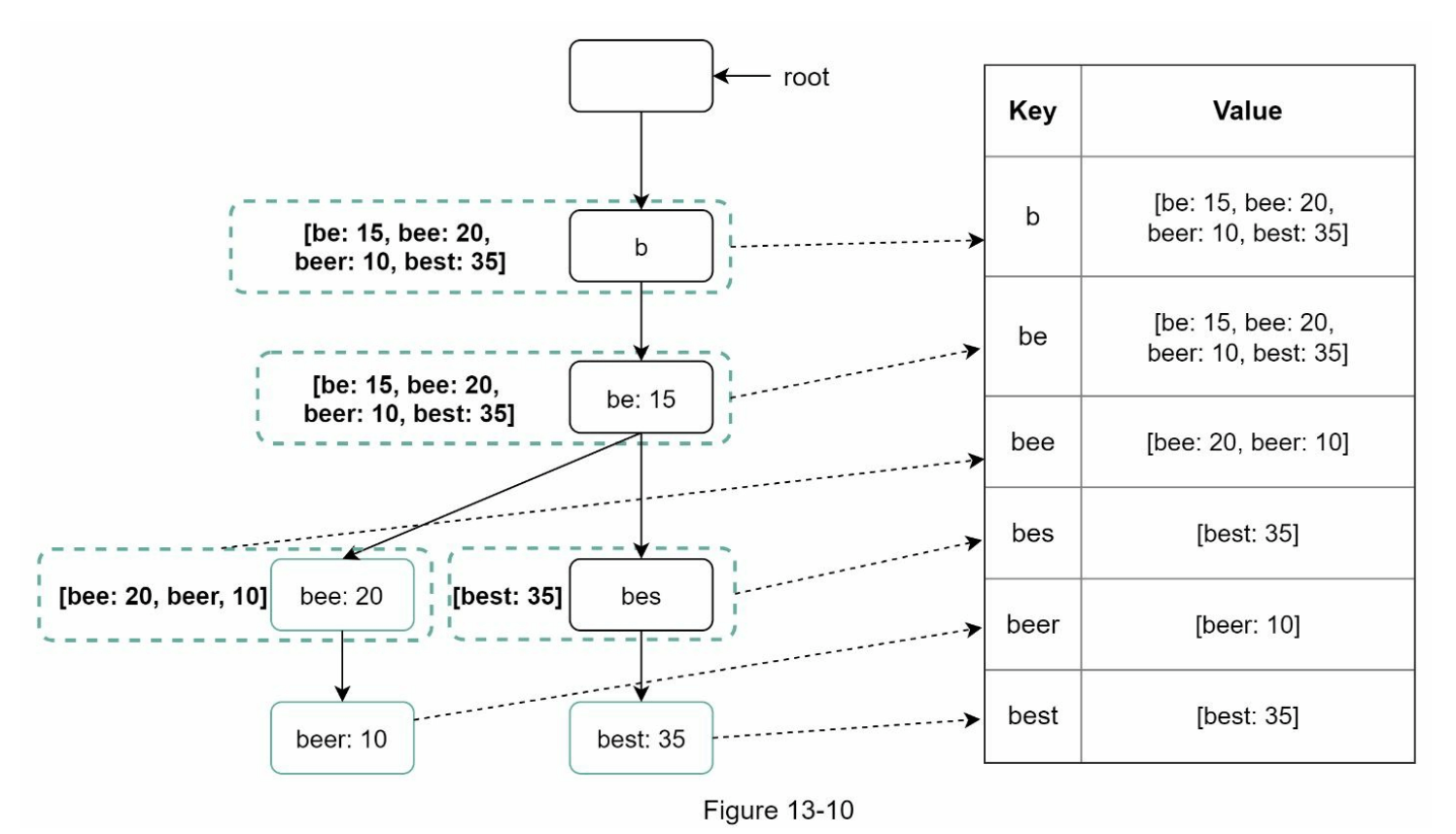
在图 13-10 中，左侧的每个字典树节点映射到右侧的 <key, value> 对。如果您不清楚键值存储的工作原理，请参阅第六章：设计键值存储。

查询服务

在高层设计中，查询服务直接调用数据库以获取前 5 个结果。图 13-11 显示了改进后的设计，因为之前的设计效率较低。

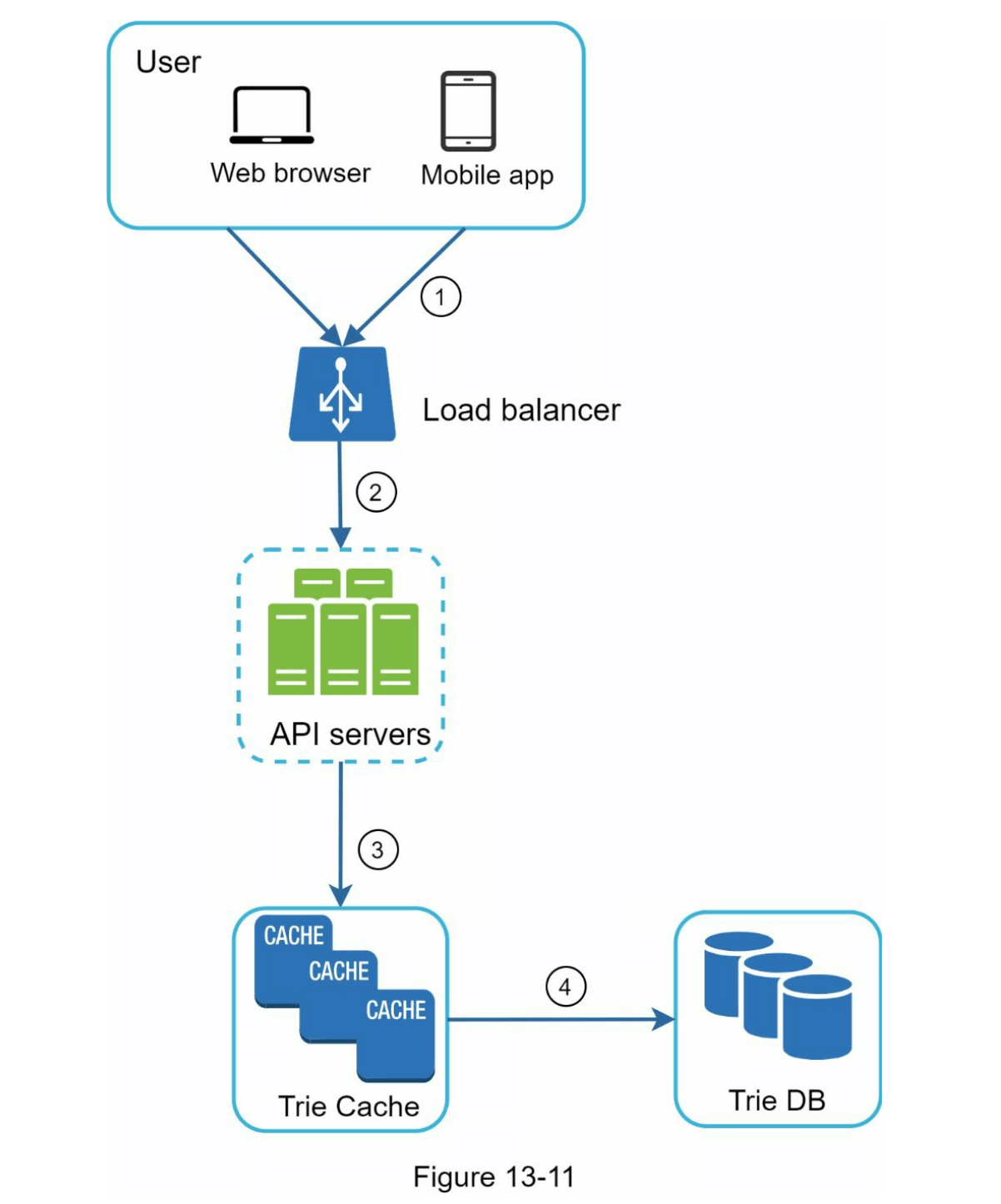
1. 搜索查询被发送到负载均衡器。
2. 负载均衡器将请求路由到 API 服务器。
3. API 服务器从字典树缓存（Trie Cache）获取字典树数据，并为客户端构建自动补全建议。
4. 如果字典树缓存中没有数据，我们会将数据补充回缓存。这样，所有后续对同一前缀的请求都将从缓存中返回。如果缓存服务器内存不足或离线，则可能会发生缓存缺失（cache miss）。

查询服务需要快速的响应速度。我们提出以下优化方案：

• AJAX 请求：对于 web 应用程序，浏览器通常发送 AJAX 请求来获取自动补全结果。AJAX 的主要优点是发送/接收请求/响应时不会刷新整个网页。

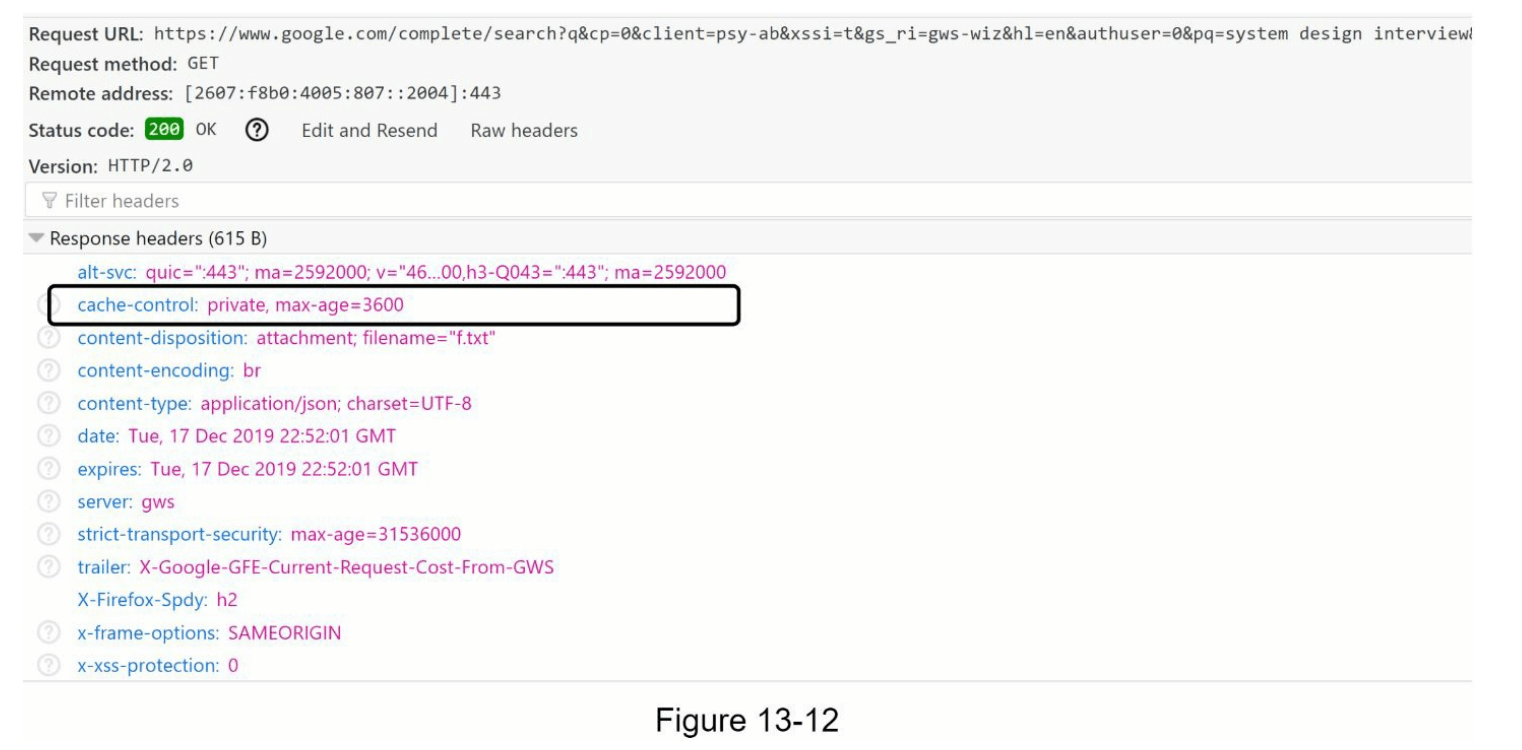
• 浏览器缓存：对于许多应用程序，自动补全搜索建议在短时间内可能不会发生太大变化。因此，自动补全建议可以保存在浏览器缓存中，以便后续请求直接从缓存中获取结果。谷歌搜索引擎使用相同的缓存机制。图 13-12 显示了当您在谷歌搜索引擎中输入“system design interview”时的响应头。可以看到，谷歌将结果在浏览器中缓存 1 小时。请注意：“cache-control”中的“private”意味着结果是针对单个用户的，不应由共享缓存缓存。“max-age=3600”表示缓存有效期为 3600 秒，即 1 小时。

• 数据采样：对于大规模系统，记录每个搜索查询需要大量的处理能力和存储空间。因此，数据采样是重要的。例如，系统仅记录每 N 次请求中的 1 次。

字典树操作

字典树是自动补全系统的核心组件。让我们看看字典树操作（创建、更新和删除）是如何工作的。

创建

字典树由工作节点使用聚合数据创建。数据的来源是分析日志/数据库（Analytics Log/DB）。

更新

更新字典树有两种方式：

选项 1：每周更新字典树。一旦创建了新的字典树，新的字典树将替换旧的字典树。

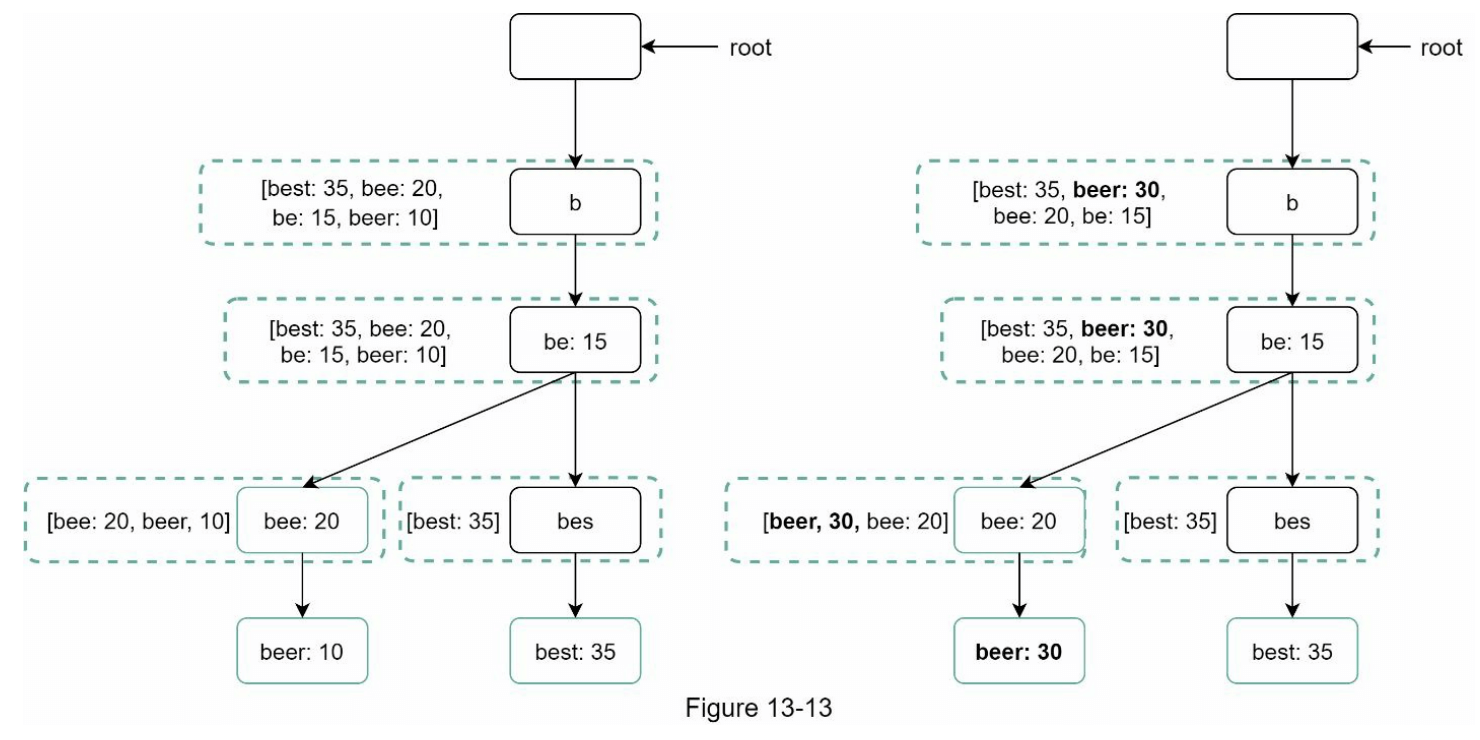
选项 2：直接更新单个字典树节点。我们尽量避免这种操作，因为它比较慢。然而，如果字典树的大小较小，这是一种可以接受的解决方案。当我们更新一个字典树节点时，所有向上的祖先节点（直到根节点）都必须进行更新，因为祖先节点存储了子节点的前查询。图 13-13 显示了更新操作的示例。左侧的搜索查询“beer”的原始值为 10，右侧更新为 30。可以看到，该节点及其祖先的“beer”值都更新为 30。

删除

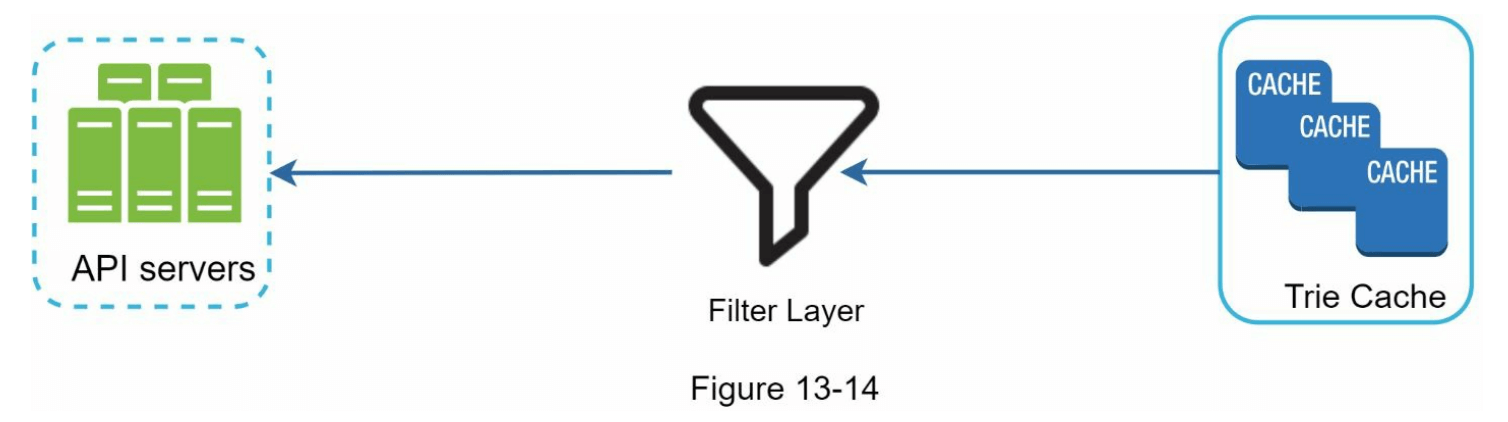
我们必须删除带有仇恨、暴力、性暗示或危险内容的自动补全建议。我们在字典树缓存（Trie Cache）前添加了一个过滤层（图 13-14），以过滤掉不需要的建议。拥有过滤层使我们能够根据不同的过滤规则删除结果。不需要的建议会异步从数据库中物理删除，以便在下一个更新周期中使用正确的数据集来构建字典树。

扩展存储

现在我们已经开发了一个系统，将自动补全查询带给用户，接下来就要解决当字典树变得太大而无法适应单个服务器时的可扩展性问题。

由于英语是唯一支持的语言，一种简单的分片方法是基于首字母进行分片。以下是一些示例：

• 如果我们需要两个服务器进行存储，我们可以将以 ‘a’ 到 ‘m’ 开头的查询存储在第一个服务器上，将以 ‘n’ 到 ‘z’ 开头的查询存储在第二个服务器上。

• 如果我们需要三个服务器，可以将查询分为 ‘a’ 到 ‘i’，‘j’ 到 ‘r’ 和 ‘s’ 到 ‘z’。

按照这种逻辑，我们最多可以将查询分片到 26 个服务器，因为英语中有 26 个字母。我们将基于首字母的分片定义为第一层分片。为了存储超过 26 个服务器的数据，我们可以在第二层甚至第三层进行分片。例如，以 ‘a’ 开头的数据查询可以分为 4 个服务器：‘aa-ag’，‘ahan’，‘ao-au’ 和 ‘av-az’。

乍一看，这种方法似乎合理，但当你意识到以字母 ‘c’ 开头的单词远多于以字母 ‘x’ 开头的单词时，这就造成了不均匀的分布。

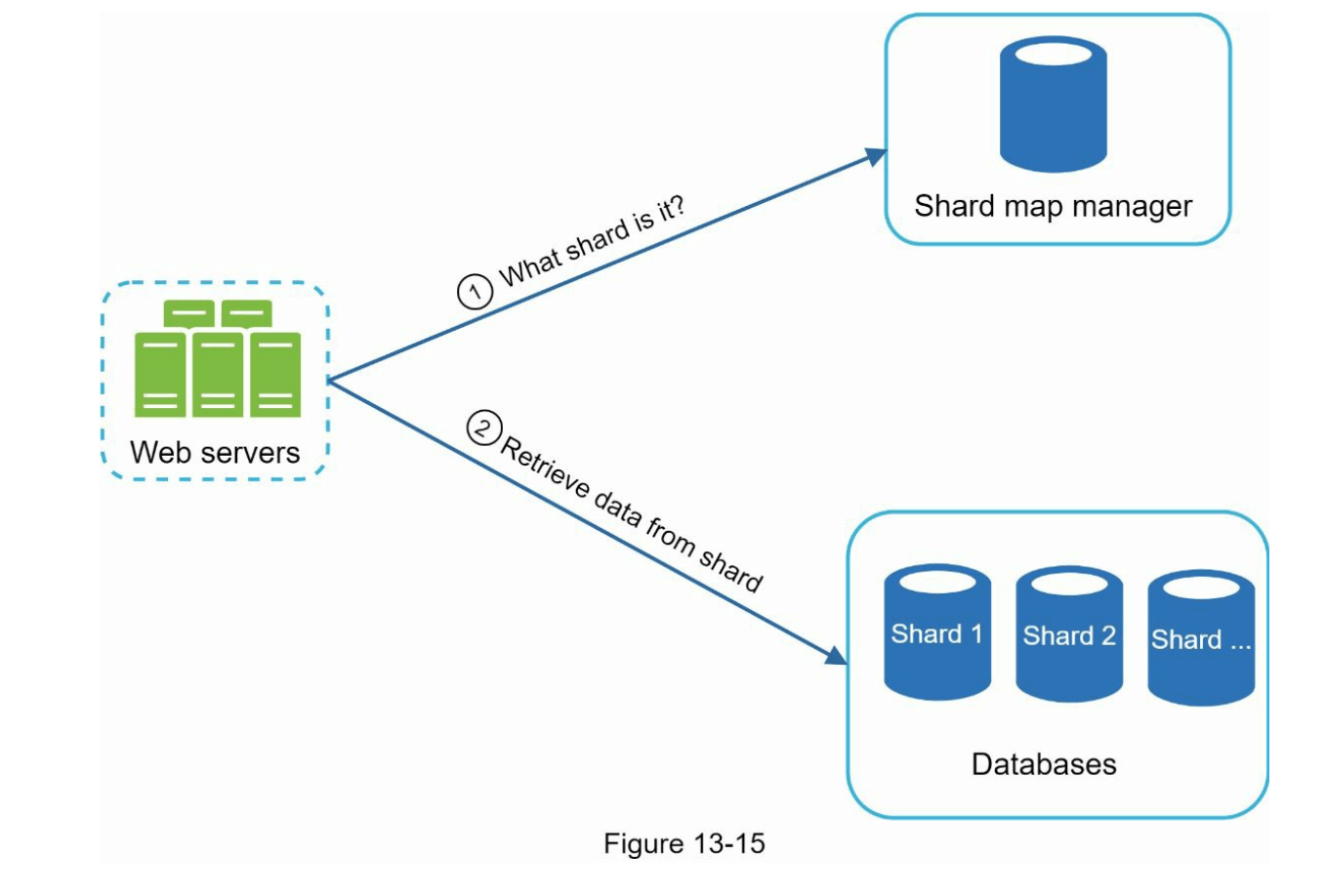
为了解决数据不平衡问题，我们分析了历史数据分布模式，并应用了更智能的分片逻辑，如图 13-15 所示。分片映射管理器维护一个查找数据库，以识别数据行应该存储的位置。例如，如果以字母 ‘s’ 开头的历史查询数量与以 ‘u’，‘v’，‘w’，‘x’，‘y’ 和 ‘z’ 合并的查询数量相似，我们可以维持两个分片：一个用于 ‘s’，另一个用于 ‘u’ 到 ‘z’ 的查询。

第 4 步 - 总结

在深入讨论结束后，面试官可能会问你一些后续问题。

面试官：你如何扩展设计以支持多种语言？

为了支持其他非英语查询，我们在字典树节点中存储 Unicode 字符。如果你对 Unicode 不熟悉，这里是定义：“一种编码标准，涵盖了现代和古代所有书写系统的所有字符” [5]。

面试官：如果一个国家的热门搜索查询与其他国家不同怎么办？

在这种情况下，我们可能会为不同的国家构建不同的字典树。为了提高响应时间，我们可以将字典树存储在内容分发网络（CDN）中。

面试官：我们如何支持热门（实时）搜索查询？

假设一条新闻事件突发，某个搜索查询突然变得流行。我们的原始设计将无法工作，因为：

• 离线工作节点尚未安排更新字典树，因为这被安排为每周运行。
• 即使安排了，构建字典树也需要太长时间。

构建实时搜索自动补全系统是复杂的，超出了本书的范围，因此我们只提供一些想法：

• 通过分片来减少工作数据集。
• 更改排名模型，并给予最近搜索查询更高的权重。
• 数据可能以流的形式到达，因此我们无法一次性访问所有数据。流处理要求一组不同的系统：Apache Hadoop MapReduce [6]、Apache Spark Streaming [7]、Apache Storm [8]、Apache Kafka [9]等。由于这些主题需要特定的领域知识，我们在这里不作详细讨论。

恭喜你走到了这一阶段！现在给自己一个鼓励，做得很好！

参考文献

[1] The Life of a Typeahead Query: https://www.facebook.com/notes/facebookengineering/the-life-of-a-typeahead-query/389105248919/

[2] How We Built Prefixy: A Scalable Prefix Search Service for Powering Autocomplete: https://medium.com/@prefixyteam/how-we-built-prefixy-a-scalable-prefix-search-servicefor-powering-autocomplete-c20f98e2eff1

[3] Prefix Hash Tree An Indexing Data Structure over Distributed Hash Tables: https://people.eecs.berkeley.edu/~sylvia/papers/pht.pdf

[4] MongoDB wikipedia: https://en.wikipedia.org/wiki/MongoDB

[5] Unicode frequently asked questions: https://www.unicode.org/faq/basic_q.html

[6] Apache hadoop: https://hadoop.apache.org/

[7] Spark streaming: https://spark.apache.org/streaming/

[8] Apache storm: https://storm.apache.org/

[9] Apache kafka: https://kafka.apache.org/documentation/